超高并发红包问题摘抄
原文地址:
业务背景和需求简介
业务中经常有直播期间播主给用户发红包的操作,由于直播场景的高实时,高并发场景。这个简单的业务中还是有不少的问题出现,这里给出一种经过验证的可以横向扩展支持超高并发量的实现手段
业务流程
主播在直播过程中向用户发送红包,主播会设定金额,红包个数,红包类型(随机红包,等额红包)。用户可以去抢那些个红包。
关键问题
生成红包的算法
其实跟发微信红包类似,播主可以发两种不同的红包。一种是等额红包,一种是随机红包。等额红包没什么技术难度,随机红包会涉及到红包的分割算法。
在随机金额的红包中为了保证用户体验,通常会允许给每份红包设定一个区间范围,保证用户得到的红包不至于太小也不至于太大。
也就是说我们需要实现如下函数, 根据红包总金额,红包个数,红包的最小值和最大值,生成一个具有n个红包具体金额的数组
def gen_red_package(amount, num, min_size, max_size) -> List[float]实现简单的红包生成算法并不难,难得是设计一个每个红包生成金额概率均等的足够公平的红包生成算法。这里可以采用一种线性分段的方法来实现均匀的红包分割,思路是这样的
我们可以先按【0,红包总金额】划定一个线段,然后我们在线段上随机位置生成n-1个点(n是红包总数)
每个生成的点与其前后的点的间隔要满足我们的金额要求
最后每两个点之间的距离就是我们要的红包金额
具体代码如下
import random
from typing import List
def gen_red_package(amount, num, min_size, max_size) -> List[float]:
amount *= 100
lines = [0, amount]
# 生成num-1个符合要求的随机的点
for i in range(0, num - 1):
loop = True
while loop:
r = random.Random().randint(0, amount)
loop = not is_valid(lines, r, min_size * 100, max_size * 100)
# 生成红包
paks = []
for j in range(0, len(lines) - 1):
paks.append((lines[j+1] - lines[j])/100)
return paks
def is_valid(arr, value, min_size, max_size) -> bool:
if arr.__contains__(value):
return False
arr.append(value)
arr.sort()
curr = arr.index(value)
l = arr[max(0, curr - 1)]
r = arr[min(curr + 1, len(arr) - 1)]
dl = value - l
dr = r - value
if dl >= min_size and dr >= min_size and dl <= max_size and dr <= max_size :
return True
arr.remove(value)
return False
print(gen_red_package(100, 5, 10, 90))⚠️注意,这种方法其实是有一定的问题存在的,假设我们想发3个总金额4块的红包,最小1块钱,最大2块钱,此时每个红包最小必须1元,有可能会生成 【1.5, 3】 然后第三个红包永远无法生成的情况,处理这种情况的方法就是调整最小红包和最大红包到一个合适的值
关于红包金额的概率公平性分析
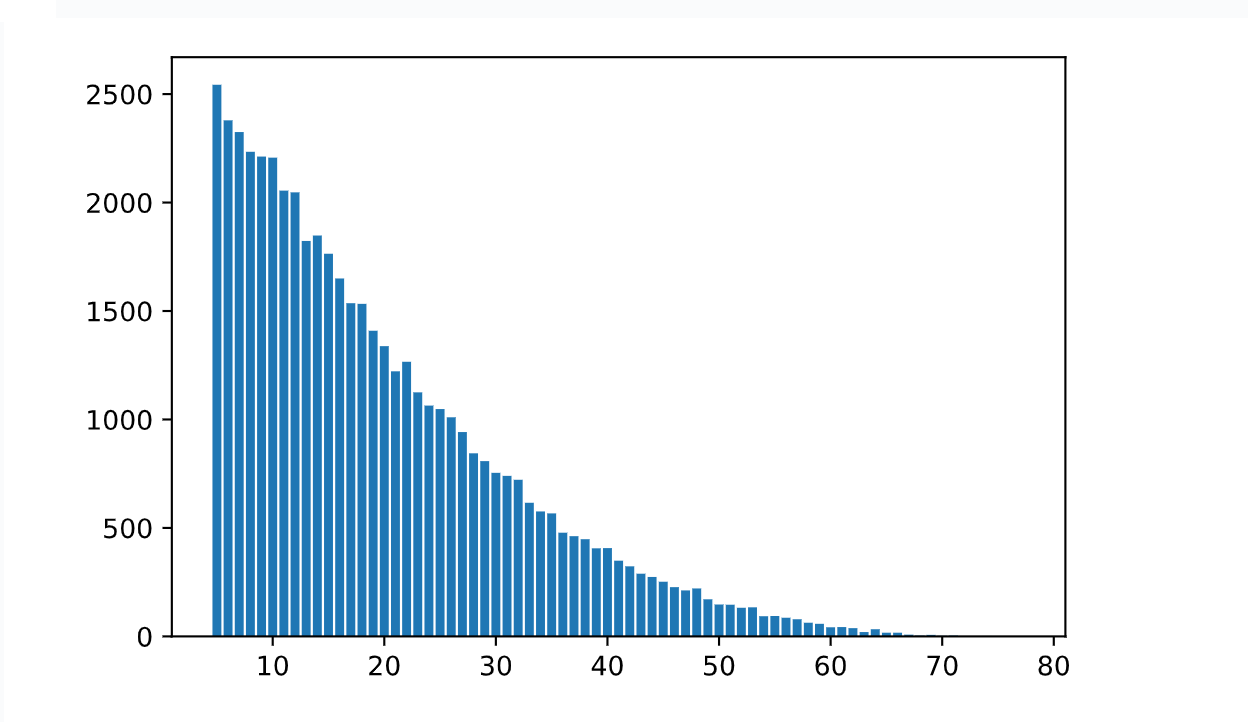
为了保证验证上面的红包算法对每个金额生成的概率均等,通过对上面的红包生成代码进行10000次测试,我们能得到如下的金额分布。我们可以看到金额在20以上的次数和在20以下的总次数是相当的。这符合我们的预期,因为我们100块钱分成5个红包,均值就是20。说明金额期望是相等的
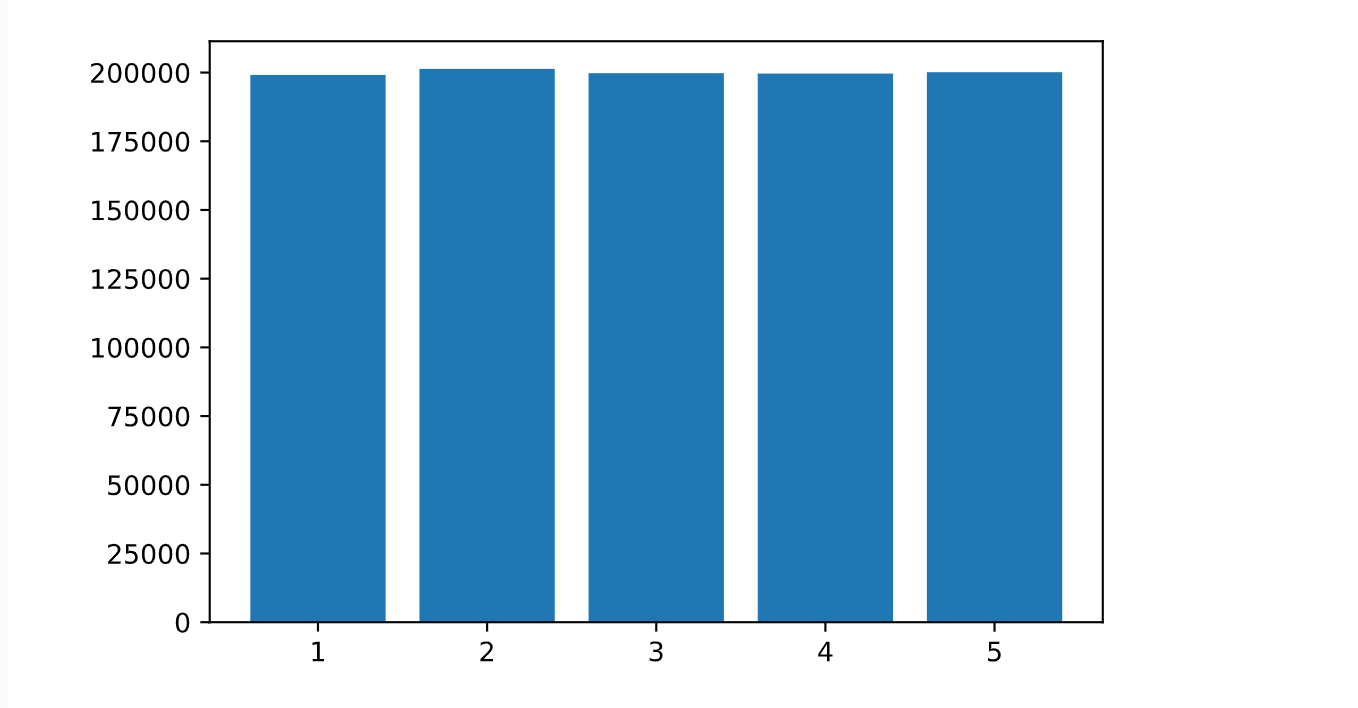
我们在看下面的各个位置的红包总金额的分布, 也能看到每个位置的总金额是差不多的, 也就是说。每个位置获取金额的大小概率是一样的。这就体现了算法的公平性,说明红包金额和抢红包的顺序没关系。
具体的分析金额生成概率的代码如下
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
"""
我们将100块钱分成5个红包, 最小5元,最大95元(这个允许的金额区间越大,算法性能越好,范围越小,越消耗性能)
"""
amount = 100
nums = 5
min_amount = 5
max_amount = 95
step = 1
stat = {}
pos = {}
for i in range(0,10000):
packages = gen_red_package(amount, nums, min_amount, max_amount)
idx = 1
for n in packages:
t = n // step
base = 1
if stat.__contains__(t):
base = stat[t] + 1
stat[t] = base
base = n
if pos.__contains__(idx):
base = pos[idx] + n
pos[idx] = base
idx += 1
fig, ax = plt.subplots()
ax.bar(np.array([i*step for i in stat.keys()]),np.array([i for i in stat.values()]));
fig2, bx = plt.subplots()
bx.bar(np.array([i for i in pos.keys()]),np.array([i for i in pos.values()]));如何处理超高并发场景下红包的分发
方案1:采用消息队列
我们可以将生成的50个红包放到redis的list中,每个用户到来,就去队列中请求弹出一个红包数据,队列数据消耗完毕, 即待分配的红包消耗完毕
这种方法实现简单, 但是会遇到并发的问题,用户去获取list的数据的时候, 由于用户的所有红包都在一个redis节点上, 所以用户的所有redis请求都会被动的落到某一个redis节点,哪怕使用集群也无法解决这种热点问题
所以在用户数据量较大的时候还是建议第二种方案
方案2: 采用数据分流
数据分流 + 用户分流:我们生成的50个红包可以分成N份,存储到不同的key上, 使用key_0-key_N存储数据会均匀的分配到redis的各个节点上。
用户在获取红包时,随机请求其中的一份红包数据,这样用户的请求可以有效打散到各个redis节点上, 同时能处理的请求数据可以随节点数量扩展, 但是这种方法的缺点也很明显, 一个是实现复杂,一个是会对用户造成一定程度上不公平的体验。
本人见解:这里说的Redis节点应该指的是Redis分布式集群,Redis分布式集群可以很大程度的提升Redis性能,而主从集群Sentinel集群则是提升可用性。
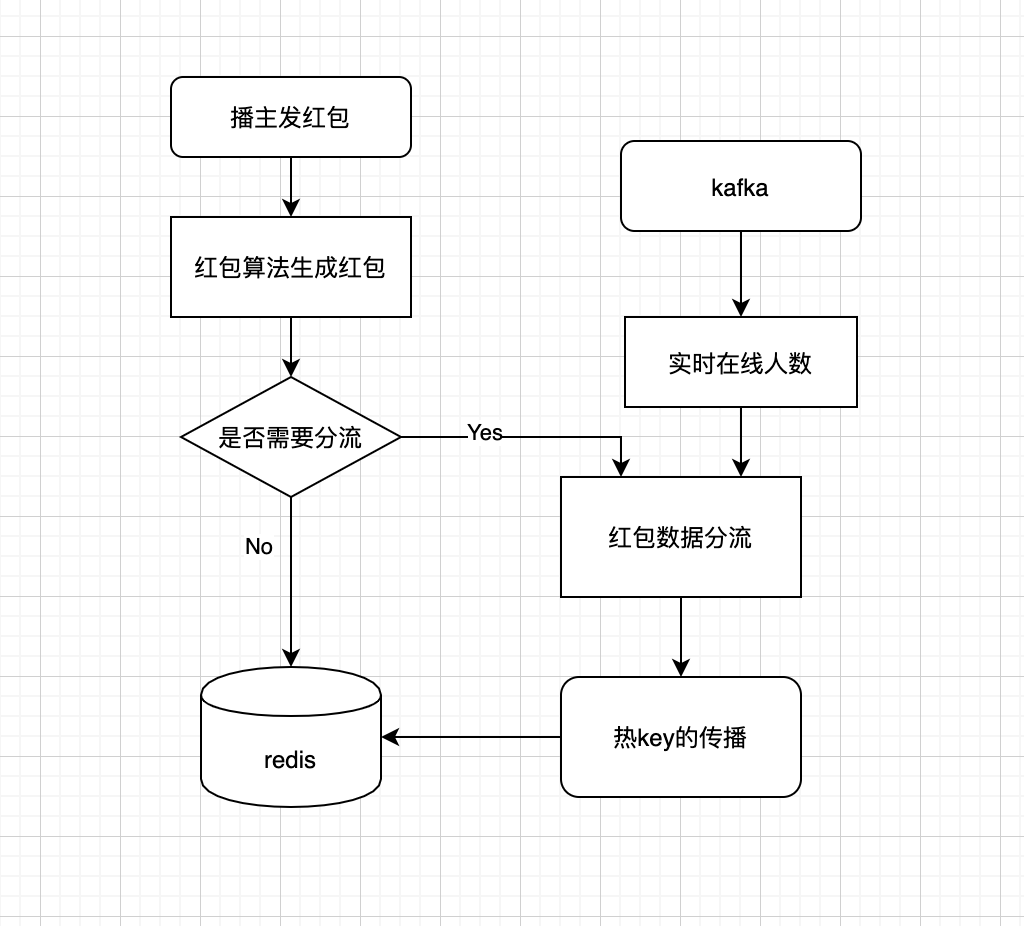
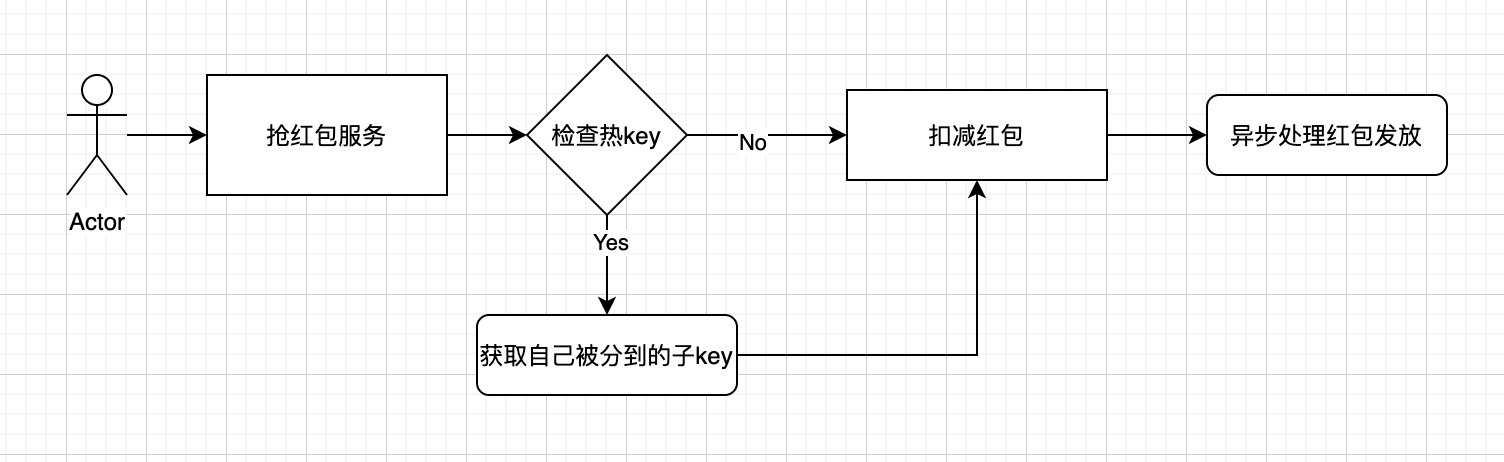
具体的红包发放流程
播主和服务端
用户端
潜在的问题:
用户存在的幻读现象
可能会出现这种情况,A,B两节点的用户请求分布不均匀,用户1请求被分流到A节点,发现A节点没有红包了,但是重新刷新,这次被分到B节点,又发现B节点还有红包可以领。解决这种问题可以采用按请求顺序轮询分发的方法,最大程度减少不公平。或者采用用户亲和的方法,根据用户的hash进行节点划分